From very early on many philosophers have given their contribution to understand the nature and constituents of matter. According to an Indian philosopher if we keep on dividing matter a stage is ultimately attained after which no longer the division occurs and the smallest form of matter will be achieved. A greek philosopher called the indivisible(cannot be divided further) matter as Atoms, but the most widely accepted theory was of John Dalton.
Dalton’s Atomic Theory : It states that whether it is an element, a compound or a mixture is composed of small particles called atoms and these atoms are indivisible particles which cannot be created or destroyed in a chemical reaction.
With the advancement in science it was observed that an atom is not the smallest particle it is actually made up of smaller subatomic particles which are responsible for its mass and neutral character.
SOME IMPORTANT UNIT CONVERSIONS
(i) 1 erg = `10^-7 J = 6.2419 xx 10^11 eV`
(ii)1 eV = `1.6 xx 10^-12 erg = 23.06 kcal mol^-1`
(iii) 1J = `6.2419 xx 10^18 eV`
(iv) 1eV = `1.602 xx 10^-19` J
(v) 1 kcal = 4.184 kJ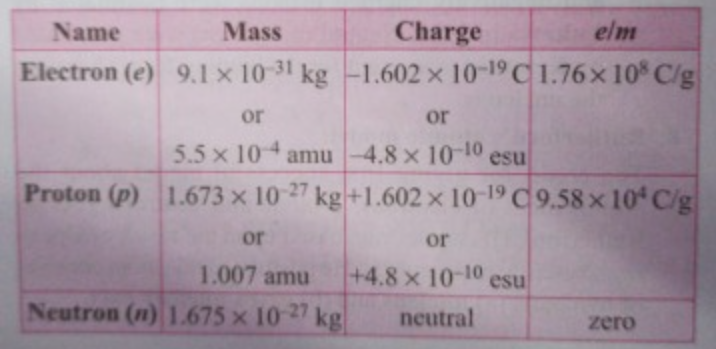

There are three major subatomic particles of an atom which are :
`***`Electrons which have negative charge
`***`Protons which have positive charge and
`***`Neutrons which have zero charge.
A. Discovery of Electron
In 1879 William Crookes studied the conduction of electricity through gases at low pressure with the help of a discharge tube. The discharge tube is closed from both the ends and has two metal electrodes and it can also be connected to a vacuum pump to adjust the pressure. When a high voltage of about 10,000 Volt was applied between the electrodes the following results were observed at different pressure.
(i) When the pressure inside the discharge tube was 1 atmosphere no flow of current was observed because gases are poor conductors of electricity (Figure a ).
(ii) When Pressure was reduced to `10^- 2` atm , a flow of current was observed between the electrodes and a coloured glow was observed (the colour of the glow depends upon the nature of gas taken) (Figure b)
(iii) When the pressure was reduced to about `10^-4` atm (0.0001 atm) the glow between the electrodes disappeared but the current was still flowing and if a perforated (containing holes) anode is used, a greenish glow was observed on the glass wall behind the anode (Figure c) this shows that some invisible rays are emitted from the cathode which pass through the pores of the perforated anode and strike the glass wall ( Usually phosphorescent material Zinc Sulphide Screen is used) these rays are called cathode rays or cathode ray particles as they are coming from cathode toward the anode.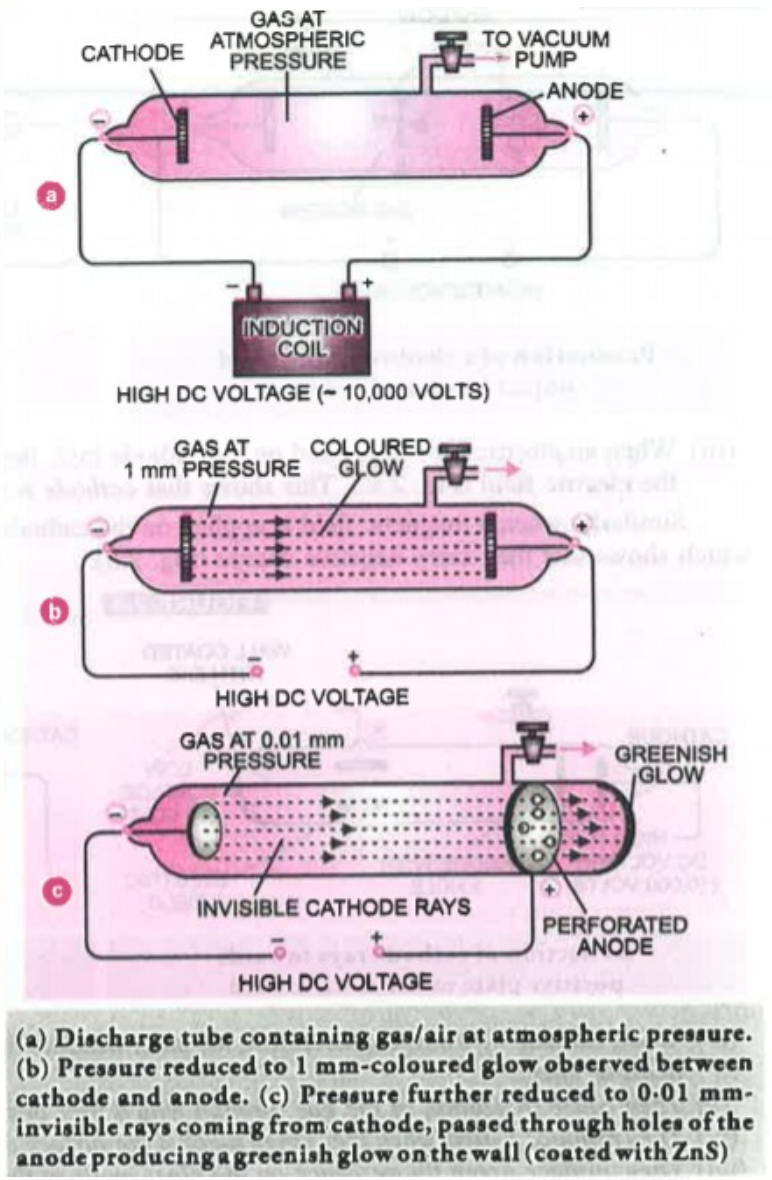

Properties of Cathode Rays
1. Gases are a bad conductor of electricity but become conductive when a high potential of approximately 10 kilo volt is applied.
2. Origin of cathode rays is a metal electrode and the gas taken inside the discharge tube is present at low pressure (`10^-2` to `10^-3`).
3. Cathode rays travel in a straight line from cathode to anode if no magnetic and electric field is present.
4. They deflect in the presence of electric and magnetic fields towards positive plate which shows that they consist of negatively charged particles called electrons.
5. When a lightweight pinwheel is placed in the path of cathode rays it starts revolving due to their mechanical nature.
6.They have an ionizing effect on the gas.
7. When they strike on the photographic plates and fluorescent material like ZnS, they produce fluorescence (produce green color on striking)
8. When beams of cathode rays strike the metal surface they produce X-rays.
9. They possess a penetrating effect that is they can easily pass through a foil of metal, they can only be stopped by the metal foils of great thickness.
Two main conclusions can be drawn from the following properties :
(i) Cathode rays carry negatively charged electrons .
(ii) Cathode rays produce mechanical effects if a small light paddle wheel is placed between the electrode it rotates; this indicates that cathode rays are made up of material particles.
J.J Thomson use different discharge tubes with electrodes of different material and different gases in the tube, he observed that the ratio of charge to mass ratio (e/m) of the electrons was same, hence it can be concluded that the charge to mass ratio for electrons is universally constant (`e/m = 1.76 xx 10^8 "coulomb/g"`)
The charge on the electron is found to be `1.6 xx 10^-19` Coulomb or `4.8 xx 10^-10 esu` by the Millikan Oil Drop experiment.
B. Discovery of proton
As we know that the atom as a whole is neutral and the atom contains a negatively charged electron so as to neutralize the negative effect there must be something positive present inside the atom, that positive charge is proton.
When high voltage was passed between the electrodes in the discharge tube, it was observed that some rays were coming from the anode which passed through the holes in the cathode and produced green fluorescence on the zinc sulphide screen, these were called anode rays or canal rays.
Origin Of Anode Rays : The anode rays are produced as a result of knockout from the electrons from the gas as a result of high speed bombardment of electrons from cathode rays on them.Thus we can say that anode rays are not produced from anode, but between the space of anode and cathode
Properties of Anode Rays :
1. They travel in straight lines, but in the opposite direction to that of cathode rays and their speed is much less than that of cathode rays.
2. They also ionize the gas and the ionising power is more than that of cathode rays
3. Unlike cathode rays their charge to mass ratio depends on the Nature of the gas and metal electrode taken in the discharge tube .
4.Anode rays also show particle nature.
5. The cathode rays contain positively charged protons.
6. They are made up of material particles.
Note - The Number of protons present in the nucleus of an atom is known as the Atomic number of the element
Atomic mass is the sum of proton and neutron present in the nucleus of an atom.
Let’s discuss about another subatomic particle which is neutron.
C. Discovery of neutron
In 1932 Chadwik discovered a subatomic particle which carries no charge that is it is electrically neutral but has mass nearly equal to that of proton which is termed as neutron

Mass Number : It is the sum of protons and neutrons present in the atom of that element, also known as atomic mass
`"Mass Number = No. of Protons + No. of Neutrons"`
Atomic Number : Atomic number is given by the number of protons present in the atom of that element .
`"Atomic Number = Total Number of Protons"`
We know that the atom is electrically neutral means the positive charge is neutralized by the negative charge and vice versa hence, we can say that the number of protons is equal to the number of electrons.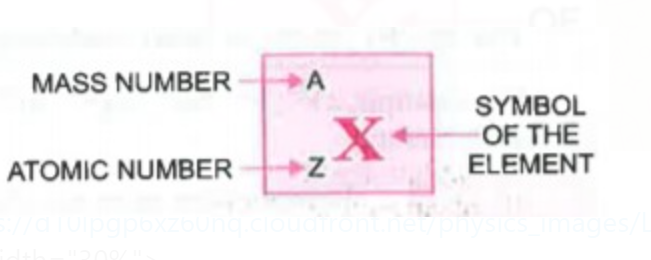

The atomic mass or mass is represented by `"A"` and atomic number is represented by `"Z"`.

Isotopes - These are those compounds in which the atomic number (Z) is the same but the mass number (A) is different.
For Example : Hydrogen isotopes having mass numbers 1, 2 and 3 respectively but each of them have the same atomic number that is equal to 1. `H_1^(1), H_1^(2), H_1^(3)` , Carbon isotopes `C _6^(12) , C_6^(14)`
Isobars - These are those compounds in which the atomic number (Z) is different but the mass number (A) is same.
For example - `Ar _18^(40), K_19^(40), Ca_20^(40)`.
Isotones - When different elements have the same number of neutrons.
For Example - `C_6^(14), N _7^(15), O_8^(16)`
They all have 8 neutrons.
Isoelectronic- Are those species which contain the same number of electrons
For example - `Al ^(+3) , O^(-2), Na^(+1)`.
`Al ^(+3)` = 13 - 3 = 10 (3 electrons are subtracted due to +3 charge)
`O^(-2)` = 8 + 2 = 10 ( 2 electrons are added due to -2 charge)
`Na^(+1)` = 11 - 1 = 10 (1 electron is subtracted due to +1 charge)

THOMSON MODEL OF ATOM

Thomson's model of atom
According to Thomson, an atom possesses a spherical shape (radius approximately `10^(-10)` m) in which the positive charge is uniformly distributed. The electrons are embedded into the positive charge in such a manner, as to give the atom most stable electrostatic arrangement . This model is known by different names for example, plum pudding, raisin pudding or watermelon. Imagine a watermelon, the red part of the watermelon is the positive charge which is distributed all over and the black seeds embedded in the red part are electrons. An important feature of this model is that the mass of the atom is assumed to be uniformly distributed over the atom.
Limitations of this model : This model was able to explain the electrical neutrality but was unable to explain how the positive charge is able to hold on the electrons inside the atom, and failed to explain the atoms stability.

RUTHERFORD MODEL

Rutherford performed the `alpha` particle scattering experiment in which he bombarded very thin (thickness ∼ 100 nm) gold foil with `alpha`–particles from a radioactive source.The thin gold foil had a circular fluorescent zinc sulphide screen around it which produces a tiny flash of light, whenever α–particles struck the screen.

Observation
(i) Most of the `alpha` particle passes through gold foil undeviated.
(ii) Very few `alpha` particles deviated at some angles.
(iii) Very few Alpha particles i.e one out of every twenty thousand particles reverted back to the original path (like a ball bouncing back after striking the wall )

Conclusions
(i) Most of the atoms are vacant (1st observation).
(ii) According to the `2^(nd)` observation, the atoms consist of a very small positive charge called Nucleus where the entire mass of the atom is considered to be concentrated that is why only some of the positively charged particles were bouncing back because both the rays and nucleus has positively charge so they repel each other, this conclusion refuted Thomson’s theory that the positive charge of the atom is spread throughout the atom.
`r_"nucleus" = 10^-5 r_"atoms"`
(iii) Rutherford calculated that the volume of the nucleus is negligible in comparison to the total volume of atom
`V_"nucleus" = 10^-15 V_"atoms"`
Note: According to Rutherford the electrons keep revolving in their orbits. As the electron revolves in its orbits the centrifugal force comes into action which balances the forces of attraction between electron and nucleus and hence prevents the falling of electron into nucleus.
On the basis of above observations and conclusions, Rutherford proposed the nuclear model of atom. According to this model:
(a) Most of the mass and all the positive charge of an atom is concentrated in a very small region called nucleus. The size of the nucleus (`10^-15`) is extremely small as compared to the size of the atom(`10^-10` m).
(b) The nucleus is surrounded by electrons, which move around the nucleus with a very high speed in circular paths called orbits hence, we can say that the Rutherford’s model of atom is similar to the model of solar system, the sun is the nucleus and the planets revolving around it are the electrons in their orbits.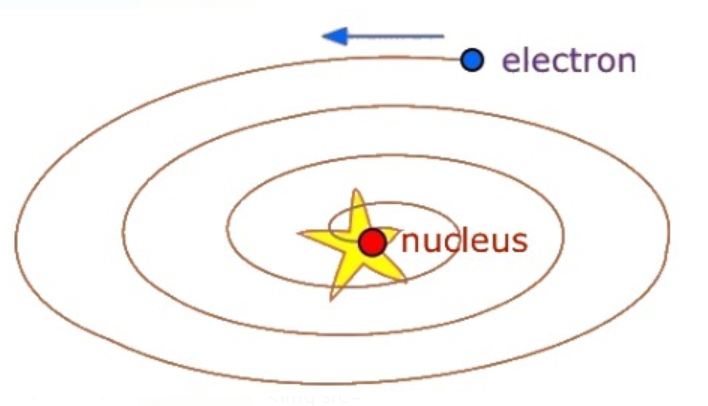

(c) Electrons and nucleus are held together by electrostatic forces of attraction
(d) Total negative charge on the electrons is equal to the total positive charge on the nucleus. As a result, the atom on the whole is electrically neutral.
(e) The alpha particles are heavy in mass and we observed that some of the alpha particles were deflected back, so their deflection was only possible if an equally heavier body is present inside the atom which is the protons present in the nucleus.

Wave nature of Electromagnetic radiation
This theory was given by Maxwell; he gave an explanation about the interaction between the charged bodies and the behaviour of electrical and magnetic fields on a macroscopic level.
Light and other forms of Radiant energy that propagates in the form of waves are called electromagnetic waves or electromagnetic radiation; these waves are produced by a charged body moving in a magnetic field or a magnet moving in an electric field.Electromagnetic waves is an important way that energy is transported in the world around us.
Characteristics of Electromagnetic Radiations
1.According to EM wave theory energy is emitted continously from a source in the form of a wave known as Radiant Energy
2. In these waves electric and magnetic fields are perpendicular to each other and perpendicular to the direction of propagation.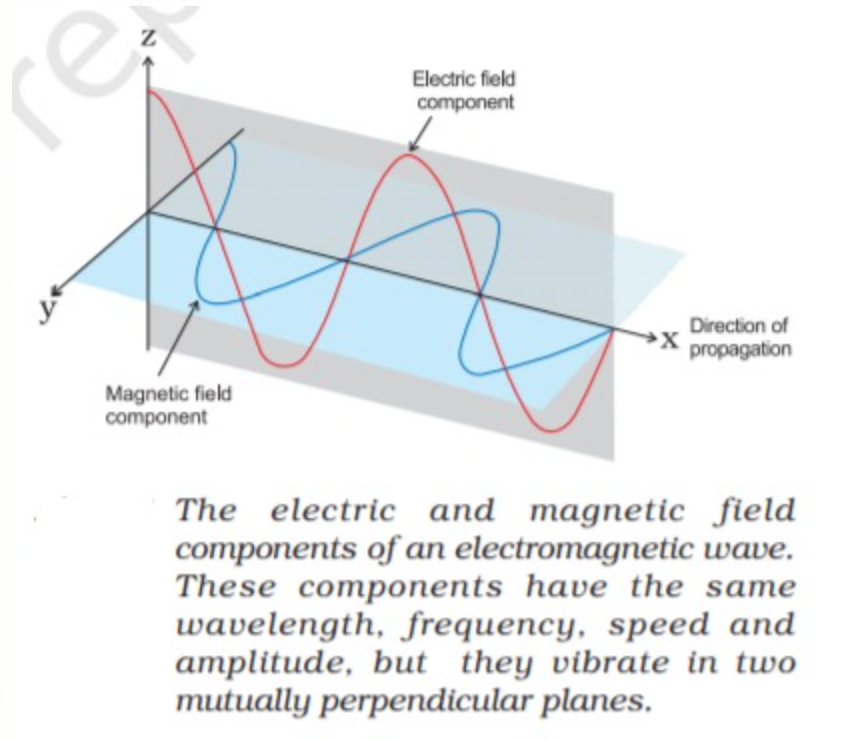

3.Do not need a medium for propagation this means that electromagnetic waves can travel not only through air and solid materials, but also through the vacuum of space..
4. These radiations are of wave character and move with the speed of light (v = `3 xx 10^8` m/s).
Important Characteristics of Wave
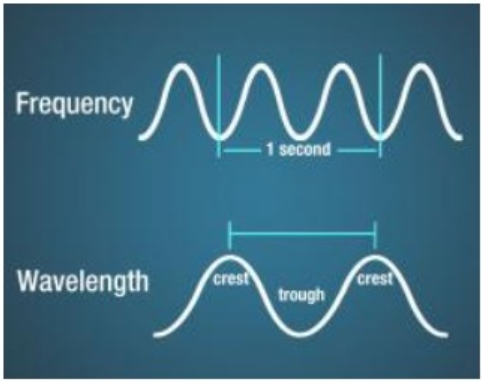
a. Wavelength : It is defined as the distance between any 2 crests or troughs, represented by `lambda` ‘lambda’.
b. Frequency : It is the number of waves passing through a point in one second ,represented by `nu` ‘nu’ and its units are Hertz or cycles/sec

c. Velocity : It is defined as the linear distance traveled by a wave in one second and is represented by ‘v’ and its units are m/s .
d. Amplitude: It is the height of the crest or depth of the trough it is represented by ‘a’ .
e. Wave Number : It is defined as the number of waves present in 1 cm of length , it is equal to the reciprocal of wavelength, represented by `bar v` its units are `cm^(-1)`.
f. Time Period : It is the time taken by one wave to pass through a point, represented by `tau` units are second (s).
`nu = ("c") / (lambda)` `" "` `bar v = (1) / (lambda)` `" "` `tau = ("1") / (nu)`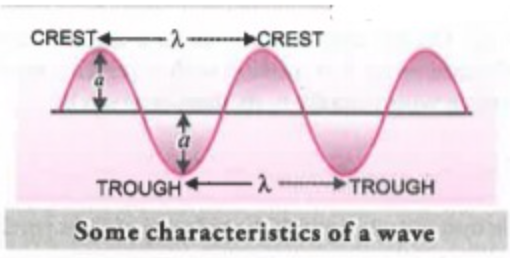

There are many types of electromagnetic radiations which differ from one another in terms of their frequency and wavelength; these all types of electromagnetic radiations constitute the electromagnetic spectrum.
Electromagnetic Spectrum
The order of wavelength is as following :
Cosmic Rays < gamma rays < X-rays < Ultraviolet rays < Visible rays < Infrared waves < Microwaves < Radio waves
As wavelength and frequency are inversely proportional the order of frequency will be the exact opposite of the previous order.

Limitations of Electromagnetic Wave Theory
Phenomenon such as diffraction, Interference were able to be explained by the help of electromagnetic theory but the wave nature of light could not justify some observation like:
(A) Black Body radiation
(B) Photoelectric Effect
(C) Variation of heat capacity of solids as a function of temperature
(D) Line spectra of atoms with special reference to hydrogen.

Black Body is an ideal body which emits and absorbs radiations of all frequencies, the radiation emitted by this bodies is called black body radiation in 1900 Max Planck give the concept of black body radiation.He stated that when solids are heated they emit radiations over a wide range of wavelength.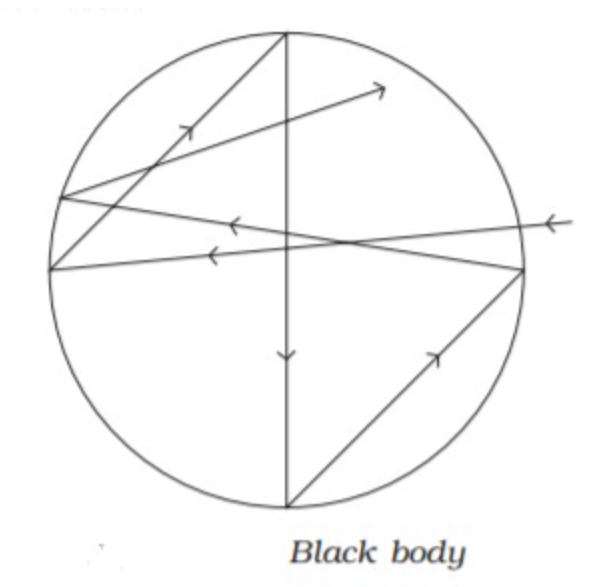

For Example We have observed that when an iron rod is heated in a furnace the rod first turns red and on further heating the colour of the rod changes to bright red to orange and yellow and progressive white then finally blue at very high temperature, this sequence of colours observed on heating of iron rod are in the sequence of increasing frequency or decreasing wavelength, these colours come under the visible range of the spectrum constituting different colours having varying frequency and wavelength of visible range of spectrum is memorized as VIBGYOR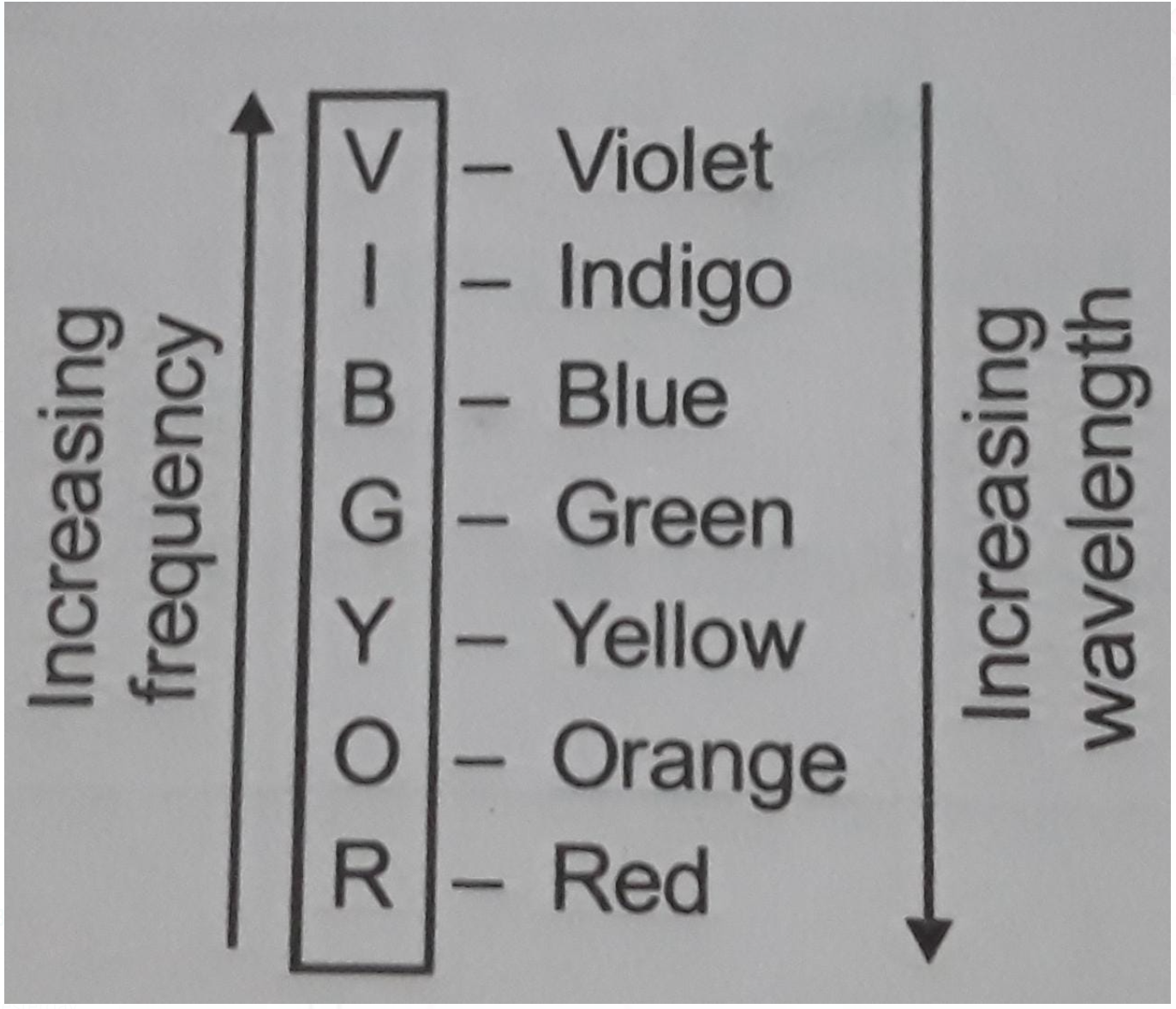

We observe that red light has maximum wavelength or lowest frequency and blue has lowest wavelength or maximum frequency, this means that when radiation is emitted it goes from higher wavelength to lower wavelength or lower frequency to higher frequency.
The intensity and frequency of emitted radiation depends upon temperature and at a given temperature the intensity of radiation emitted increases with decrease of wavelength reaches a maximum value at a given wavelength and then starts decreasing with further decrease of wavelength.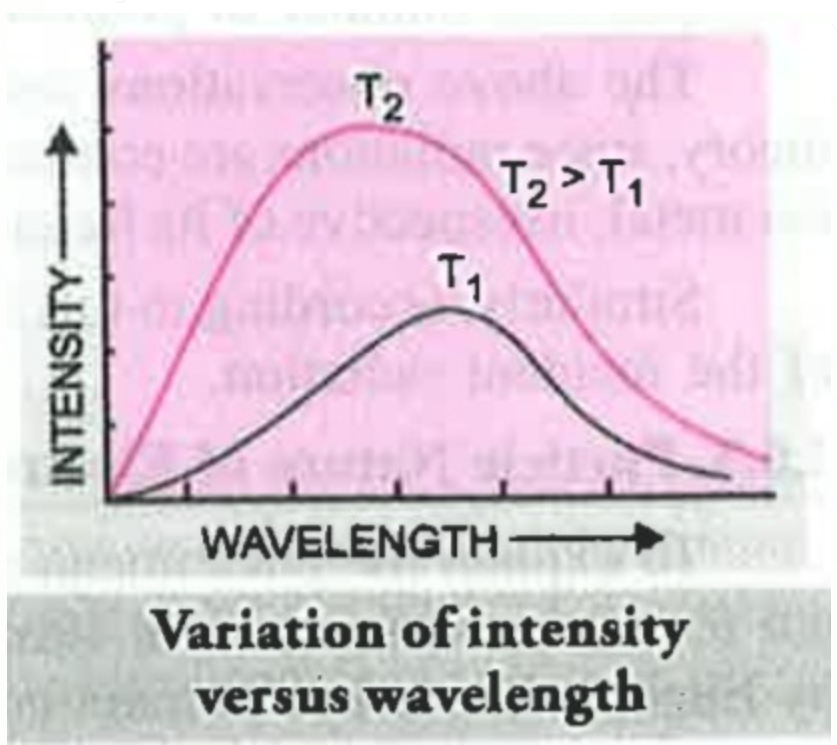

Planck suggested that the energy which is emitted or absorbed by the black body is discontinous and suggested that atoms and molecules could emit or absorb energy only in discrete quantities and not in a continuous manner. He gave the name quantum to the smallest quantity of energy that can be emitted or absorbed in the form of electromagnetic radiation.

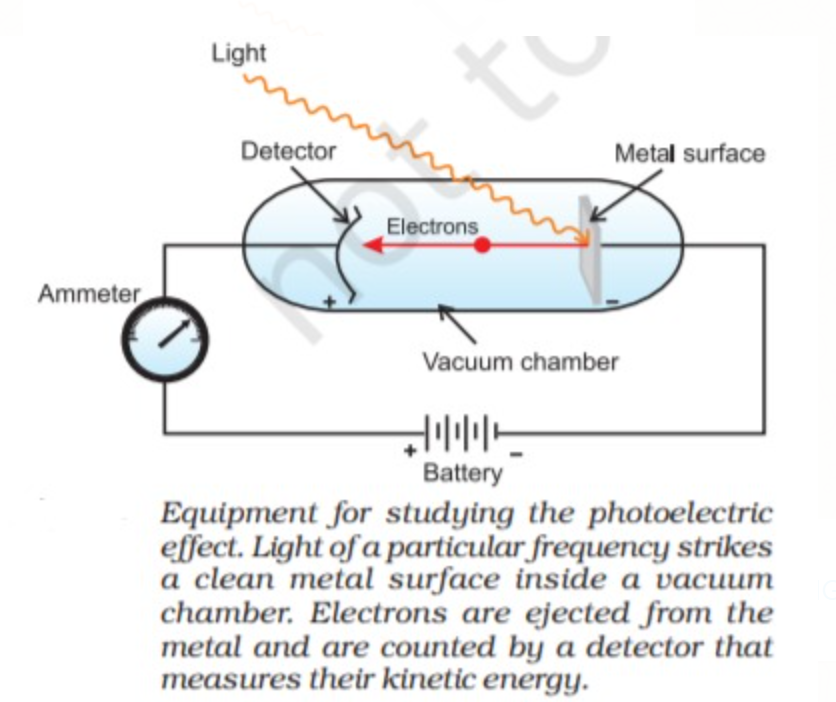
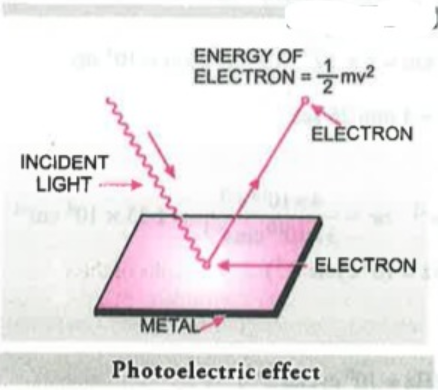
H. Hertz exposed certain metals such as potassium, rubidium, caesium etc.to a beam of light with high frequency and observed ejection of electrons. This phenomenon of ejection of electrons due to a beam of light is called the Photoelectric effect. The results observed in this experiment were:
1. There is no time lag between the striking of light and ejection of electrons; it means that as soon as the light of suitable frequency (Here suitable frequency means a light of frequency greater than threshold frequency) strikes the metal surface, photoelectrons are ejected without any delay.
2 .Threshold frequency is the minimum frequency of light that is needed to cause Photoelectric effect that is for the ejection of electrons below this frequency the photoelectrons cannot be ejected threshold frequency is represented by `nu_0` (Every metal has their different threshold frequency).
3. The number of photoelectrons ejected is proportional to the intensity of light striking the metal but it does not depend upon the frequency of light.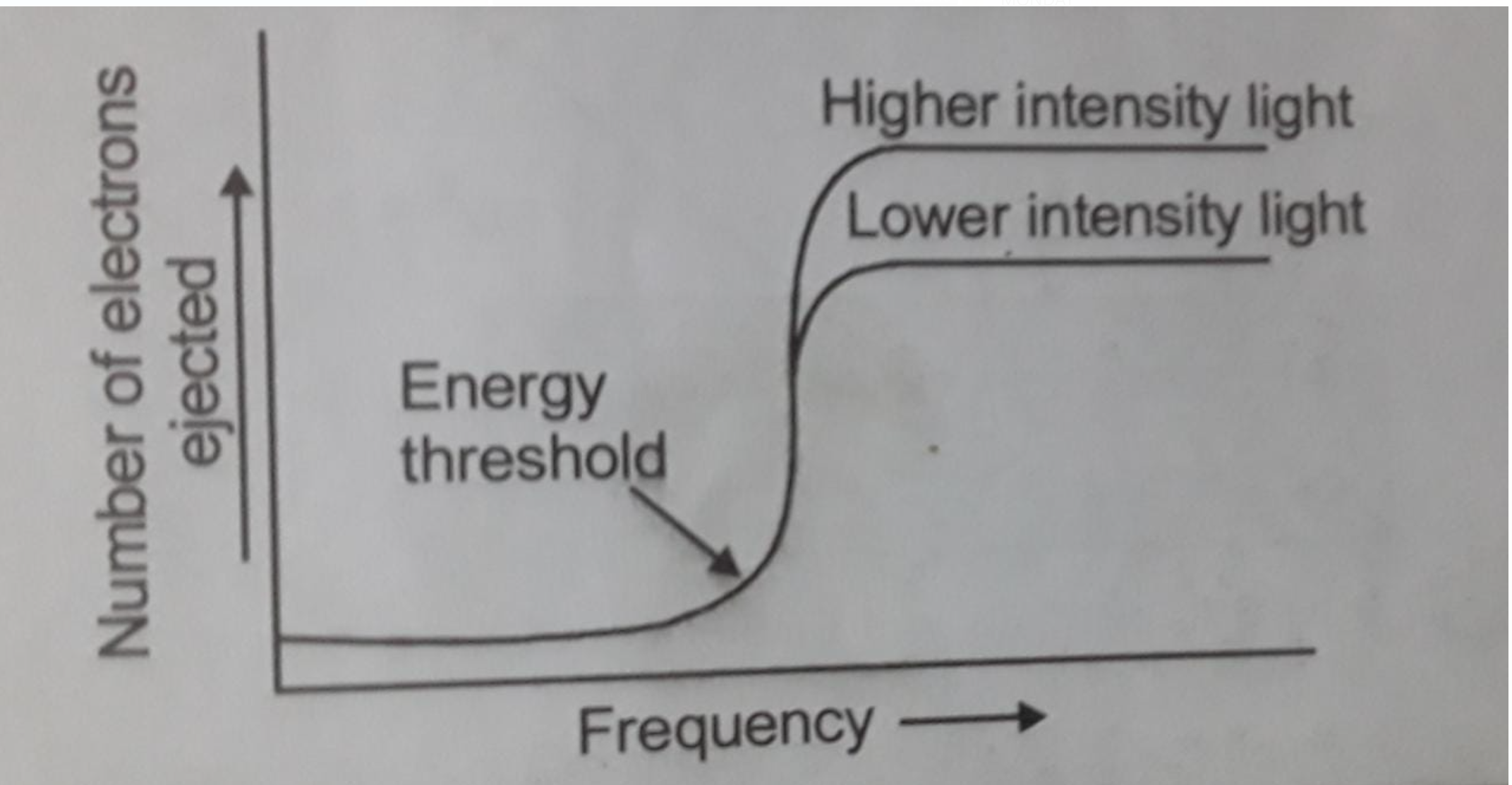

4.The kinetic energy of the ejected electrons depend upon the frequency of light used and not on the intensity.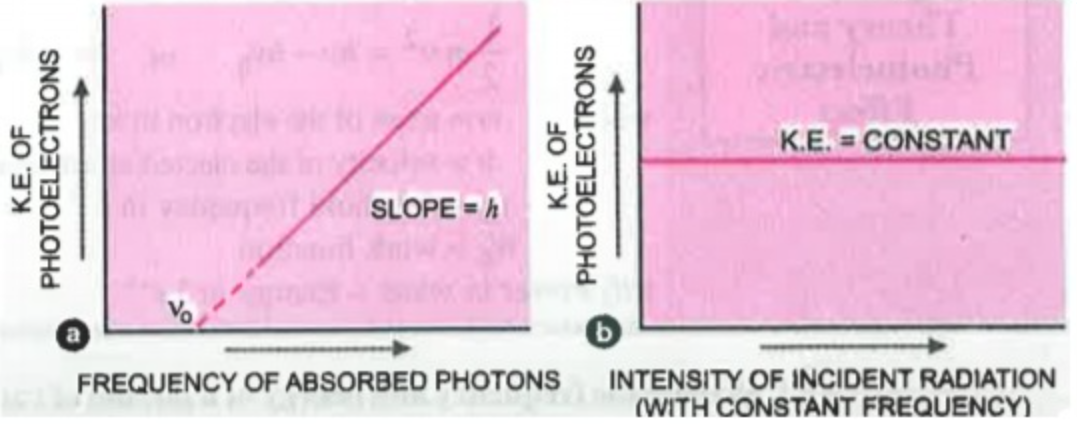

Graph a can be explained by using the straight line equation : `y = mx + c`..(i)
Let us write the photoelectric equation in this form : `K.E_(max)` = h`nu` - h`nu_0`..(ii)
Now as we compare eq (i) and eq (ii) we can see that
`K.E_(max)` = y
h = m (slope)
`nu` = x
`- h nu_0` = c (intercept)
Explanation for photoelectric Effect
Einstein explained the Planck's Quantum theory of electromagnetic radiation on the basis of energy conservation, when a photon having sufficient energy strikes with the electron on the metal atom it transfers its energy instantaneously to the electron during the collision and the electron gets ejected without any delay or time lag but some amount is consumed in overcoming the forces of attraction between the nucleus and electrons and when an electron is ejected then it collides with other fellow electrons also hence this process also consumes some amount of energy, hence the Kinetic Energy is not maximum, but theoretically we take `K.E_max` and greater the energy possessed by the photon greater will be the transfer of energy to the electron and greater will be the kinetic energy possessed by the photoelectron.The energy supplied by the photon is used in overcoming the threshold energy and the remaining is used to eject electrons with maximum kinetic energy
Energy of Striking Photon = Threshold energy + Kinetic Energy of the ejected Electron
Energy of Striking Photon (E) = `h nu`
Threshold energy = `h nu_0` `" "` Work function = `w_0` `" "` (The threshold energy = Work Function)
`:.` = `h nu = h nu_0 + ("1") / ("2") m_e v^2`
This equation can be written in many ways.
` K.E _max` = `h nu` - `h nu_0`
` K.E _max` = `h c ( ("1")/ (lambda) - ("1") / (lambda_0))`
`lambda` is wavelength of light and `lambda_0` = Threshold wavelength .
The threshold wavelength can be defined as the maximum wavelength of light required for the ejection of electrons during photoelectric effect.

According to Planck, energy is not emitted continously but in the form of small packets called quanta that are absorbed or emitted in the form of electromagnetic radiation, and in case of light the quanta is known as Photon. The energy (E ) of a quantum of radiation is proportional to its frequency (`nu` )
`E prop nu` `therefore` `E = h nu` `" "` `rArr` `"E" = ("hc") / (lambda)`
h = Planck's Constant = `6.626 xx 10^(-34)` Js
Hence, it can be concluded that more the wavelength lesser the energy and as frequency and energy have direct relation so more the frequency more the Energy. The total amount of energy emitted or absorbed will be some whole number quanta i.e `E = n h nu` (n= any integer)

The phenomenon of Black body radiation and photoelectric effect, explains the particle nature of light but in order to explain the phenomenon of diffraction and interference the wave nature of light was necessary, so a conclusion was made that light behaves like a wave as well as a particle. When radiation interacts with matter it displays particle like properties and while when it propagates it displays waves like properties. Light is a kind of radiation so it have both wave as well as particle character .

As a beam of light passes from one medium to another it gets deviated or refracted from its original path because speed of light depends upon the nature of the medium through which it passes.
When a ray of white light is passed through a prism, the wave with shorter wavelength bends more than the one with a longer wavelength. Since ordinary white light consists of waves with all the wavelengths in the visible range, a ray of white light is spread out into a series of coloured bands called spectrum.
The light of red colour which has longest wavelength is deviated the least while the violet light, which has shortest wavelength is deviated the most.The spectrum of white light, that we can see, ranges from violet to red such a spectrum is called continuous spectrum.In a continuous spectrum we can see the different colors merge into each other such as in the rainbow.

Emission Spectrum
When the radiation emitted from some source such as the sun, or by passing electric discharge through gas at low temperature or by heating a substance at high temperature is passed directly through a prism and then received on a photographic plate such spectrum is known as Emission Spectrum. Depending upon the source of radiation the emission spectrum is of two types :
(a) Continuous Spectrum: When light from any illuminating source such as a bulb or the sun is passed through a prism and it splits into seven different bands of colors ranging from Violet to Red, such spectrum is known as Continuous Spectrum.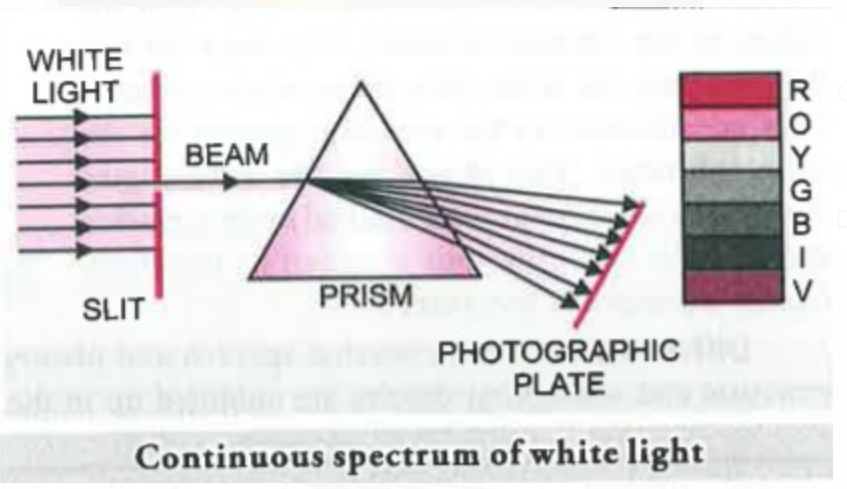

(b) Line Spectrum : When some volatile salt is placed in the Bunsen flame or an electric discharge is passed through a gas at low pressure, light is emitted. The colour of light emitted depends upon the nature of substance, For Example, sodium or its salts emit yellow light while potassium or its salts give out violet light. If this light is resolved in a spectroscope, it is found that no continuous spectrum is obtained but some isolated coloured lines are obtained on the photographic plate separated from each other by dark spaces. This spectrum is called ‘Line emission spectrum’ or Line spectrum.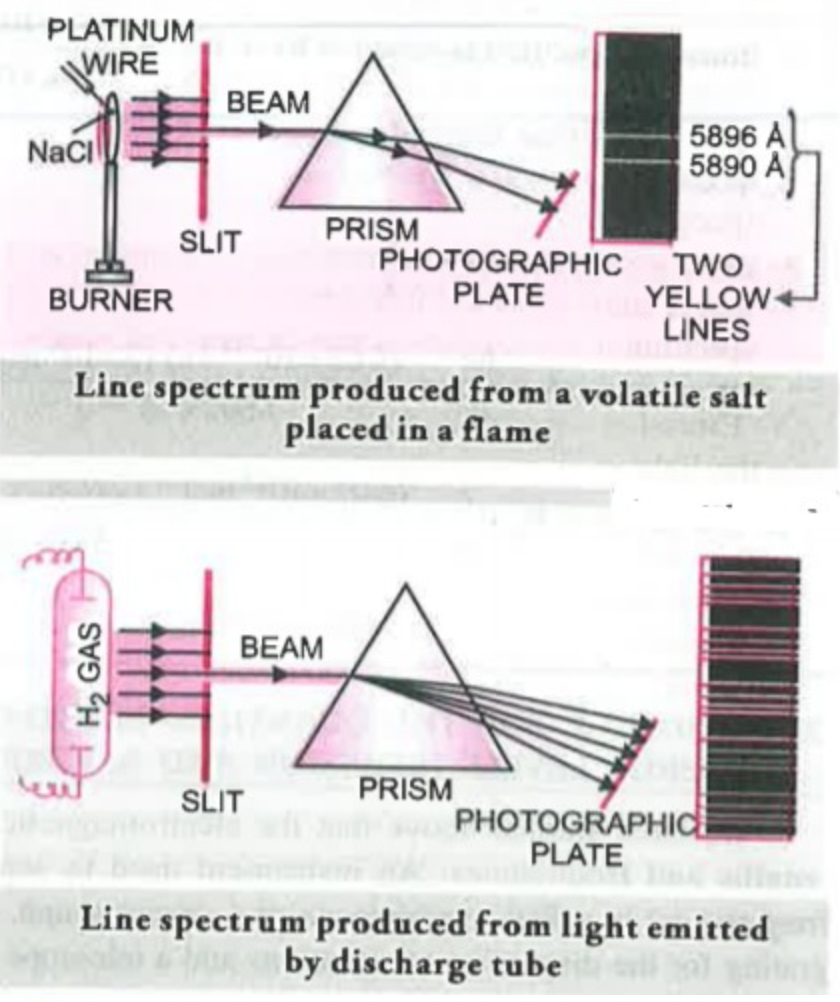

The line spectrum of every element is unique just like every person's finger prints are different no two person have identical finger prints similarly no two elements can have same Line Spectrum.
Absorption Spectrum
An absorption spectrum is like the photographic negative of an emission spectrum.When white light is passed through the solution or vapours of a chemical substance, we observe some dark lines in the spectrum which is usually continous. The dark lines are formed because when the light passes through the substance it absorbs some wavelength depending on the substance. The dark lines were observed in the same place as light lines were formed in the case of emission spectrum when the case is of same substance. This shows that the wavelengths absorbed are same as that were emitted in the emission spectra.

Line Spectrum of Hydrogen
The line spectrum of Hydrogen is discontinous and discrete i.e. no overlapping of spectral lines occurs.It is a kind of Emission Spectrum and is obtained by passing an electric discharge through hydrogen gas at low pressure.Hydrogen molecule splits up into atoms.These electrons absorb the energy and get excited and when these excited electrons come back to ground state they emit electromagnetic radiation of discrete frequencies.
The spectral lines are expressed in terms of ` bar v`
To calculate the wavelength of light emitted (This formula was derived by Rydberg)
` (1) / (lambda) = bar v = 109,677 ( (1) / (n_1^2) - 1 / (n_2^2))`
`n_1` = 1,2,3,4 and `n_2` = `n_1` + 1
This is known as Rydberg’s Formula
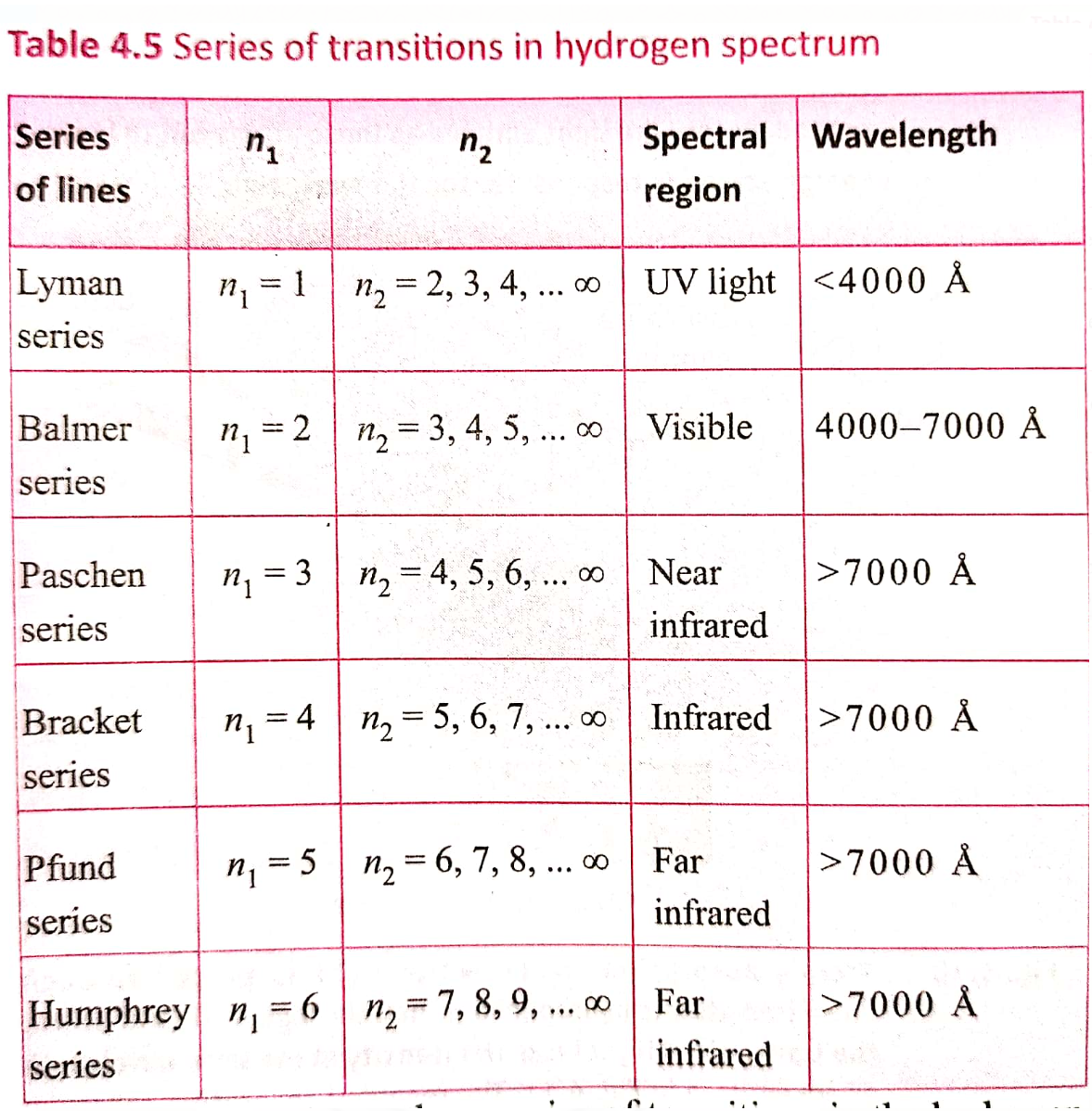
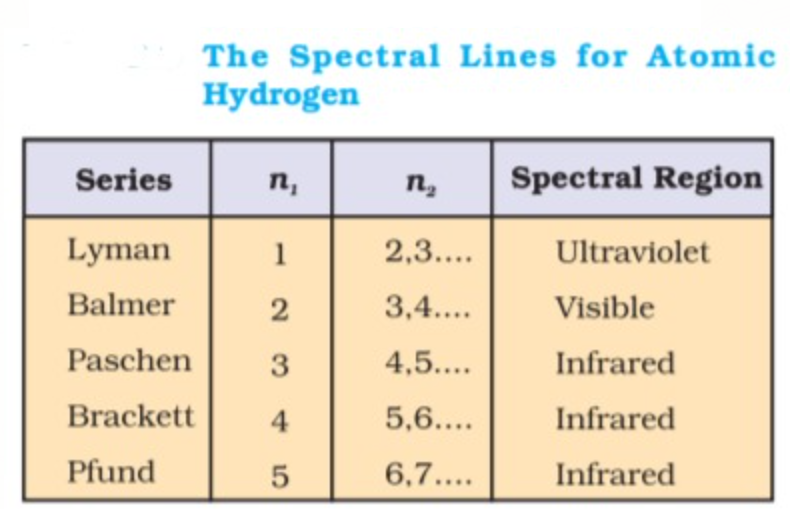
The value 109,677 `cm^-1` is called the Rydberg constant. The first five series of lines that correspond to `n_1` = 1, 2, 3, 4, 5 are known as Lyman, Balmer, Paschen, Bracket and Pfund series, respectively.
For Lyman series, `n_1` = 1, `n_2` = 2, 3, 4…
For Balmer series, `n_1` = 2, `n_2` = 3, 4, 5…
For Paschen series `n_1` = 3, `n_2` = 4,5, 6…
For Brackett series `n_1` =4, `n_2` = 5, 6,7...
For Pfund series, `n_1`= 5, `n_2` = 6, 7, 8.... For Hydrogen like particles the formula is`" "` `bar v = 109,677 ( (1) / (n_1^2) - 1 / (n_2^2)) xx Z^2`
When `n_1` = 2, the expression given above is called Balmer’s formula as it was first put forward by Balmer to explain the series of lines bearing his name (i.e., lines in the visible region).
Limiting line : The limiting line of any spectral series in the hydrogen spectrum is the line when `n_2` in the Rydberg formula is infinity, i.e., `n_2` = `infty`,

(i) Inability to explain the stability of atom : According to Electromagnetic theory, when a charged particle revolves it should emit energy continuously so electron must radiate energy and should collapse but this does not happen and the electrons keep on revolving, hence he could not explain the stability of atoms.
(ii) Inability to explain the line spectra of the elements : According to Rutherford energy is emitting continuously so spectrum must be continuous but observed spectrum was found to be discontinuous. Bohr’s theory was also unable to explain the splitting of spectral lines in the presence of magnetic field (Zeeman effect) or an electric field (Stark effect)..
(iii) Inability to describe distribution of electrons and energies electron: It was unable to explain how the electrons are distributed around the nucleus and what were their energies..

Niels Bohr proposed a new model based on Planck’s Quantum theory.
Postulates
1. Electrons revolve in circular path, Orbit or shell which are stationary and discontinuous . The term Stationary used here is not because the electrons are stationary but because they are non radiating and no energy loss occurs while revolving and energy does not change with time.
a. Energies of different stationary states in case of Hydrogen are given by Bohr's Formulae
`E_n = - (2 pi^2 me^4) / (n^2 h^2)` `" "` It can be written in various other ways
`E_n = (- 21.8 xx 10^-19) / (n^2)` J / atom`" "` = `- (13.6) / (n^2)` eV / atom`" "` = `- (1312) / (n^2) kJ mol^-1`
For Hydrogen like species (Those species which have one electron only) such as `He^(+)` , `Li^(+2)` , `Be^(+3)`
`E_n` = `- (13.6) / (n^2) xx Z^2` eV / atom `" "` `E_n` = `- (1312) / (n^2) xx Z^2` kJ `mol^-1`

(b) The radii of stationary states for Hydrogen atom are given by
`r_n = a_0 n^2` `" "` `a_0 = 0.529` `A^@` or 52.9 pm or 0.0529 nm
For hydrogen like species : `r_n = (a_0 n^2) / (Z)`
(c) The velocity of electron in different orbits is given by :
`upsilon_n = upsilon_0 / (n^2)` `" "` `upsilon_0 = 2.188 xx 10^8` cm `s^-1`
For hydrogen like species : `upsilon_n = upsilon_0 xx ("z") / (n^2)`
2 .Electrostatic force between electron and nucleus provides sufficient centripetal force.
` (K z e^2) / (r_n^2) = (m V_n^2) / (r_n)`
3. The angular momentum and energy of an electron is quantised i.e only discrete values are present.
`m""v""r = ("nh") / (2pi)` `" "` n = 1, 2, 3....
m is the mass, v is the tangential velocity of the revolving electron and r is the radius of the orbit. We can say that the angular momentum of the electron can be `(h) / (2 pi)` ; `(2h) / (2 pi)` ; `(3h) / (2 pi)`
Quantisation of Electronic Energy: The concept of quantisation can be understood in this way that for example you hire a taxi, then while the taxi is moving its speedometer is also moving according to the acceleration and it can have any random value such as 42,57,93 e.t.c whereas the fare meter can have only some specified values such as 5, 10, 15 etc that means the fare is quantised similarly when we say that energy is quantised we mean that it does not have any random value.
4.When electrons are revolving in their normal energy state they revolve without losing any energy and this state is known as Ground State
5. Energy is emitted or absorbed only when electrons jump from one state to another,for instance an electron jumps from ground state to higher state called Excited State when it is subjected to high temperature. After some time the electron jumps back to the lower energy level by emitting energy in the form of light of suitable frequency.
The amount of energy emitted or absorbed is given by the difference of energies of two energy levels i.e.
`Delta E = E_2 - E1`
`E_1` = Energy of lower orbit `" "` `E_2` = Energy of higher orbit
6. The frequency of radiation absorbed or emitted when transition occurs between two stationary states that differ in energy by` ∆E`, is given by:
`nu = (∆E) / ("h") = ( E_2 - E_1 ) / ("h")`
De - Merits of Bohr’s Model
1. It is applicable only for mono-electronic species.
2. It cannot justify the quantisation of angular momentum.
3. He couldn’t explain the Heisenberg Uncertainty Principle.
4. According to Bohr the electrons are moving in circular paths which was wrong.
5. Spectrum of Protium and Deuterium were not found to be similar.
6.Under high spectral resolution spectral lines were observed, to be splitted called fine line spectrum so, the model was unable to explain Zeeman and Stark effect which is splitting of spectral lines in magnetic and electric field respectively

According to De Broglie, matter like radiation should also exhibit dual behaviour i.e. both particle and wave like properties.
De Broglie, gave the relation between wavelength (λ) and momentum (p) of a material particle
`E = h nu` (According to Planck)
`E = m c^2` (According to Einstein)
`h nu = m c^2`
But as we know `nu = ("c") / (lambda)` `" "` `:.` `h ("c") / ( lambda )` = `mc^2` or `lambda = (h) / (mc)` `" "` m = mass of photon `" "` c = velocity of photon
De Brogile replace mass of photon with mass of particle and velocity of photon with velocity v of material. Hence,
`lambda = ("h") / ("mv") = ("h") / ("p")`
Calculation of De Brogile wavelength of the electron from the potential applied to accelerate it
As Kinetic Energy = `("1")/ ("2") m v ^2` `" "` `:. v = sqrt (("2E ")/ ("m") ` `" "` `:. lambda = ("h") / ("mv")` = `("h") / ("m") sqrt ("m") / (2 E) = ("h") / (sqrt ( 2 m E ))`
Further `"Kinetic Energy"` = `"Charge" xx "Potential difference"` i.e K.E = eV `" "` `lambda = ("h") / sqrt (2 m eV)`
By substituting the values we can get the wavelength of an electron as
`lambda = (1.226 xx 10^-9) / sqrt (V)` m

According to Heisenberg Uncertainty Principle it is not possible to determine the position and momentum of a microscopic particle simultaneously ,
`Delta x . Delta p >= ("h") / (4 pi)`
`Delta x` = Uncertainity in position
Minimum uncertainity will always be equal to `("h") / (4 pi)`.
`Delta p` = Uncertainity in momentum
As we know that momentum = `mass xx velocity`
`Delta p` = m `Delta v`
`Delta x . m Delta v >= ("h") / (4 pi)` = `Delta x xx Delta v >= ("h") /(m. (4 pi))`
Explanation
If we try to measure the position of the electron, to see its position we need small wavelength. We know that light consists of photons. So. photons strike the electron, the reflected photon in the form of light reaches our eye and this way we are able to know the position of the electron.We know that the electron is a point charge and almost dimensionless, therefore to know its position we must use wavelength smaller than the dimensions of the electron. Therefore shorter the wavelength,will give greater the accuracy.
But shorter wavelength is associated with high frequency and high energy.
`"Energy" prop ("1") / (" wavelength")`
Therefore when this high energy photon strikes the electron, it changes the speed as well as direction of the electron i.e. momentum changes.Thus, it is clear that momentum cannot be found with certainity in this case, but position is known.

Quantum mechanics is that branch of science which takes the wave as well as particle nature of matter into consideration. This model is the most accepted model based on the concept of probability concept.
The probability of finding an electron in Hydrogenic atom(Hydrogenic species are the ones which contain a single electron like Hydrogen) is :
Schrodinger Wave Equation: Schrodinger gave the equation for wave motion of electron around the nucleus he put forward an equation :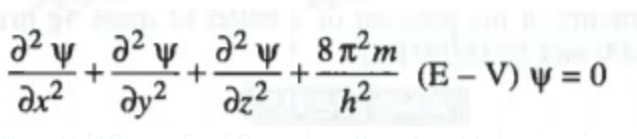

E = Total Energy, V = Potential Energy, `psi` = Amplitude of the wave
After solving the Schrodinger Wave Equation we get the values of E and `psi` and E is the value of quantised energy which the electrons can have and `Psi` is the value of wave functions. De Brogile, Heisenberg Uncertainty Principle,and Schrodinger gave this model together, and discarded Bohr’s Model.
Orbital is the region where the probability of finding an electron is maximum(upto 90%).
Characteristics of Quantum Model of Atom
1. In this model electrons have been described as a 3D wave under a positively charged nucleus.
2. The amplitude of this electron wave is given by wave function `psi` Has no physical significance related to the probability of finding an electron.
3. `psi^2` is called probability density which gives the probability of finding an electron at a point around the nucleus it is always positive.
`psi` has 2 parts :
a. Radial Part - Depends on n, l
b. Angular Part - Depends on m, l
Note :1. For s subshell, l = 0 m = 0 therefore, `psi` is independent of angular wave function.
2. Electron clouds are the space around the nucleus which describes the probability of finding an electron it is shown in the form of dots.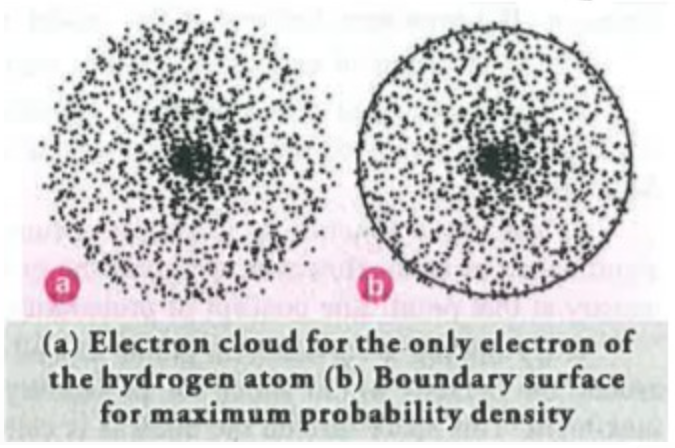

3. The probability of finding an electron is never zero even at very large distances there is a small possibility.

Quantum Numbers can be defined as the index number which is required to designate an electron in an atom .We know that an atom consists of a large number of orbitals but these orbitals are different from each other on the basis of their size, shape and orientation in space. The characteristics of an orbital are expressed in the terms of three Quantum numbers called Principal, Azimuthal and Magnetic quantum number. An electron is designated with the help of four Quantum numbers the three which we have earlier mentioned and the fourth one is Spin quantum number. In simple terms the quantum numbers tell the address of electrons. For example
Suppose you are travelling by train then the Train station(Nizammudin or New Delhi) will be the Principal Quantum Number the Train(Shatabdi, Rajdhani e.t.c.) would be the azimuthal quantum number the coach of the train would be the Magnetic quantum number and the berth number would be the spin quantum number
Suppose we use the quantum numbers to tell our location,country we live in would be the Principal Quantum Number, the state we live in would be the, azimuthal quantum number the district we live in would be the, Magnetic quantum number and the sector or block we live in would be the spin quantum number.
Let us discuss more about these four quantum numbers.
PRINCIPAL QUANTUM NUMBER
It is represented by 'n' Principal quantum number informs us about the energy level or shell to which the electron belongs and can have any integral value except 0, n = 1,2,3,4,5,6……
Various principal energy levels are also designated by K,L,M,N,O,P…..
Information given by Principal quantum no. :
1. Principal Quantum Number gives the average distance of the electron from the nucleus and greater the n greater is the atomic size.
2. It gives information about the energy of electron with increase in 'n' the energy of electron increases, it can also be shown by the following formulae of Energy of the electron in `n^(th)` shell
`E_n = - ( 2 pi m e ^4) / ( n^2 h^2 )` in this formulae though E and n have inverse relation which might confuse us, that E is inversely proportional to n but we need not forget the minus sign on the right hand side so as n will increase the right side value as a whole will increase and hence energy will increase.
3.It gives information about the angular momentum of an electron present in the orbit.
`( m v_n r_n) = ( n h ) /( 2 pi )`
2. Azimuthal Quantum Number/ Subsidiary Quantum Number/ Angular Momentum Quantum Number
It is represented by l and gives the following information
1. It gives us information about the number of sub shells or sublevels of energy within the same principal shell.
2.Information about the shape of the subshell.
3.Used to calculate the angular momentum of the electron present in any sub shell.
Angular momentum of electron in orbital = `sqrt (l (l+1)) (h ) / (2 pi)` hence the value of orbital angular momentum depends only upon the value of l therefore 1s, 2s ,3s will have the same values because their n are different but l is same
Each value of l represents a different subshell and depending upon the value of l that is l = 0, 1, 2, and 3 different subshells are designated as s, p, d and f respectively.
Azimuthal Quantum number gives information about the energy associated with various orbitals along with the value of n, the energy of various orbitals is decided by the n + l rule.

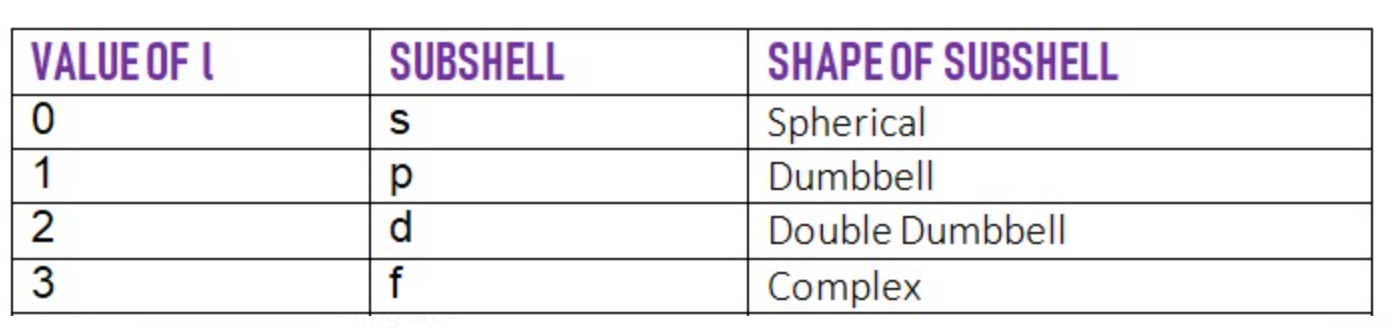
The value of l lies between 0 to n - 1 ( l < n) it can never be equal to or greater than n.
For the first shell (K), n = 1 , l can have only one value = 0
For the second shell (L), n = 2 , l can have 2 values = 0,1
For the first shell (M), n = 3 , l can have only three value = 0,1,2
For the first shell (N), n = 4 , l can have only three value = 0,1,2,3
A single orbital can have only two electrons

In case of s sub-shell l =0 `therefore` No. of orbitals = 1 `" "`No. of electrons = 2
For p sub-shell l =1 `therefore` No. of orbitals = 3 `" "`No. of electrons = 6
For d sub-shell l =2 `therefore` No. of orbitals = 5 `" "`No. of electrons = 10

Suppose if n = 1
Sub - shells = 1 i.e K sub shell
Orbitals = `n^2` = 1
As one orbital can have only two electron and in this case only one orbital is present, hence the number of electrons = 2
Suppose if n = 2
Sub - shells = 2 i.e L sub shell 2s (one) and 2p (three)
Orbitals = `n^2` = 4 = 2s (one) and 2p (three)
As one orbital can have only two electron and in this case 4 orbitals are present, hence the number of electrons = 8
Suppose if n = 3
Sub - shells = 3 i.e M sub shell 3s , 3p, 3d
Orbitals = `n^2` = 9 = 3s (one) 3p (three), 3d(five)
As one orbital can have only two electron and in this case 9 orbitals are present, hence the number of electrons = 18
Suppose if n = 4
Sub - shells = 4s, 4p, 4d, 4f
Orbitals = `n^2` = 16 = 4s (one), 4p(three), 4d(five), 4f(seven)
As one orbital can have only two electron and in this case 16 orbitals are present, hence the number of electrons = 32
Magnetic Quantum Number A magnetic spin quantum number is represented by `m_l`.
It gives information about the orientation of the subshell; this quantum number is used to explain the Zeeman effect.
The Zeeman Effect is the splitting of a spectrum line into several components by the application of a magnetic field.

When an electron revolves around the nucleus it generates an electric field and this electric field in turn produces a magnetic field,this internal magnetic field interacts with the external magnetic field. Under the influence of this external magnetic field the electrons of subshells orient themselves in certain preferred regions of space around the nucleus called orbitals. Orientation is the splitting of subshells in three dimensions
The value of m lies between -l to + l and for every value of l, m has (2l + 1) values.
(i) For l = 0 (s subshell) m can have only one value, m = 0 This means s subshell has only one orientation.
(ii) For l = 1 (p subshell) m can have 3 values i.e. m = -1, 0, +1.
(iii) For l = 2 (d subshell) m can have 5 values i.e. m = -2, -1, 0, +1, +2.
(iv) For l = 3 (f subshell) m can have 7 values i.e. m = -3, -2, -1, 0, +1, +2, +3.

Spin quantum number Electron revolves around the nucleus as well on its own axis, this gives rise to the spin quantum number.This quantum number gives information about the direction of spinning of the electron present in any orbital. It is represented by s or `m_s`, the electron can revolve in any direction whether clockwise or anticlockwise hence the spin quantum number can have only two values + 1 / 2 and - 1 / 2 and represented by ``upward arrow (`uparrow`) and downward arrow (`downarrow`) respectively.

The spin quantum number helps us to magnetic properties of substances Such as the ferromagnetic ,paramagnetic and diamagnetic nature of elements and compounds.
Note :
1. Shell: Represents the main energy level occupied by electron.
Given by Principal Quantum number 'n'.
2. Sub-Shell : Represents the sub - energy level occupied by the electron.
It is given by Azimuthal quantum number 'l'.
For a given value of n, l= O to n-1.
3. Orbital : Represents the orientation of sub-shell under the influence of magnetic field.
Represented by Magnetic Quantum Number `m_l` .

s ORBITALS
s orbitals are spherical in shape, and the probability of finding an electron is equal in all directions so they are symetrical . For s orbital the azimuthal Quantum number l = 0 and the magnetic quantum number m = 0,thus s can have only one orientation.

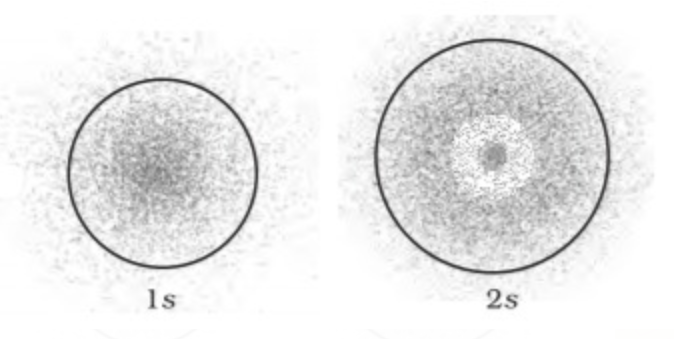
The size and energy of s orbital increases with increasing value of principal quantum number ‘n’ .
1s < 2s < 3s < 4s
p ORBITALS
Orbitals are dumbbell shaped for p orbitals (l = 1) There are three possible values of m i.e. m = 0 , - 1 , +1, this means that there are three p orbitals whose axes are mutually perpendicular these are designated as `p_x`, `p_y`, `p_z` depending upon whether the electron density is maximum at X-axis, Y-axis, Z-axis and are directional in nature, p- orbitals are equal in shape,size and energy but their orientation is different.

In p orbitals the size and energy increases with increase in principal quantum number.
4p > 3p > 2p
d - ORBITAL
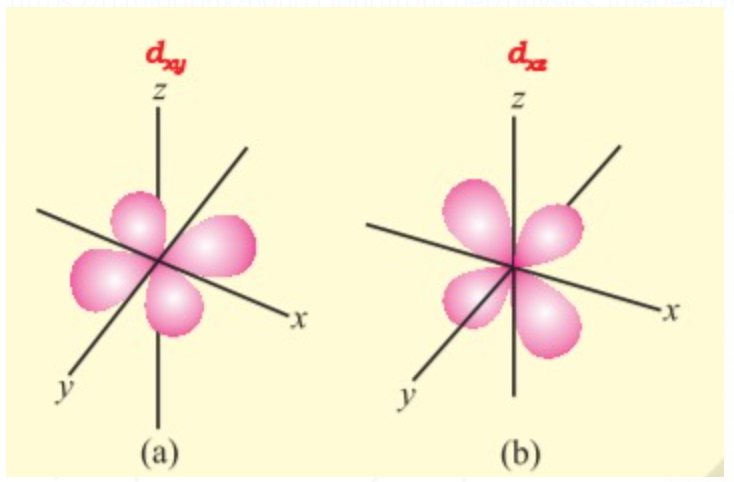
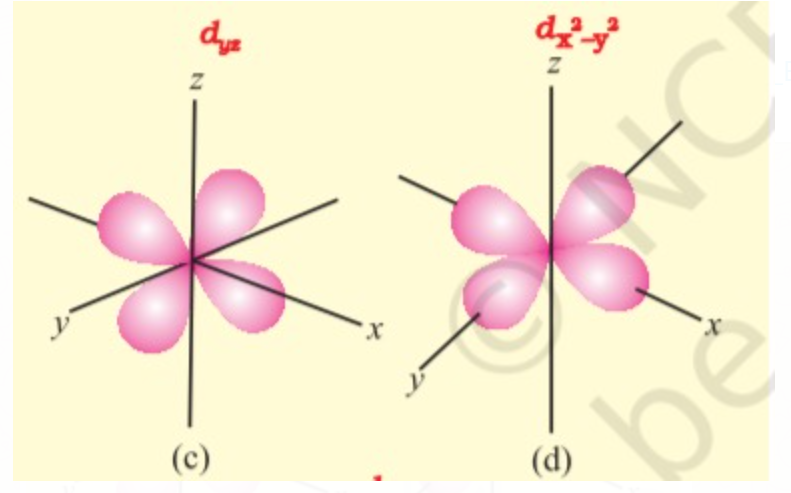
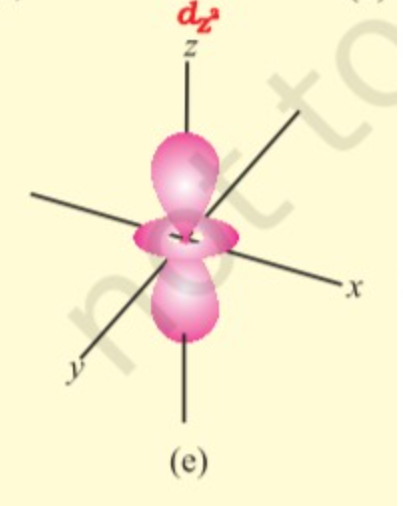
d orbitals have double dumbbell shaped except `d_z^(2)` which has a baby shooter-like shape. For d- orbitals l = 2 there are five possible values of m i.e. m = -2, -1, 0, +2, +1, hence it has 5 orbitals which are designated as `d_(xy), d_(yz), d_(xz), d_x^(2) - y^(2), d_z^(2)` .
`" "` `" "`

For a hydrogen atom that contains only one electron the energy of that electron is just dependent upon the value of principal quantum number n and the energy of the electron increases when Principal Quantum Number increases, therefore the order of energies would be 1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f <......
The orbitals having same energy such as 2s and 2p ; 3s ,3p and 3d are called degenerate orbitals.
The 1s orbital in a hydrogen atom, corresponds to the most stable condition and is called the ground state and an electron residing in this state is most strongly held by the nucleus. An electron in the 2s, 2p or higher orbitals in a hydrogen atom is in an excited state.
Energy of an electron in a Multi - Electron Atom
In case of multi electron atoms the energy of an electron depends on both the principal quantum number (n) and the azimuthal quantum number(l) hence we can say that the energy of an electron depends upon the subshell of the principal shell to which the electron belongs that is, for a given principal quantum number, s, p, d, f ... all have different energies.
Some important observations from energy level diagram of multielectron atoms may be made as follows :
(i) Within a given principal quantum number, the energy of orbitals increases in the order `s lt p lt d lt f`
(ii) The subshells of a particular shell do not have equal energies, e.g., 2s and 2p have different energies.
(iii) In a particular shell, a subshell with lower value of l has lower energy. Thus, in the second shell, 2s (l = 0) has lower energy than 2p (/ = 1). Similarly, in the 3rd shell, energies are in the order : 3 s<3 p<3d and in the 4th shell, they are in the order : 4s<4p<4d<4f .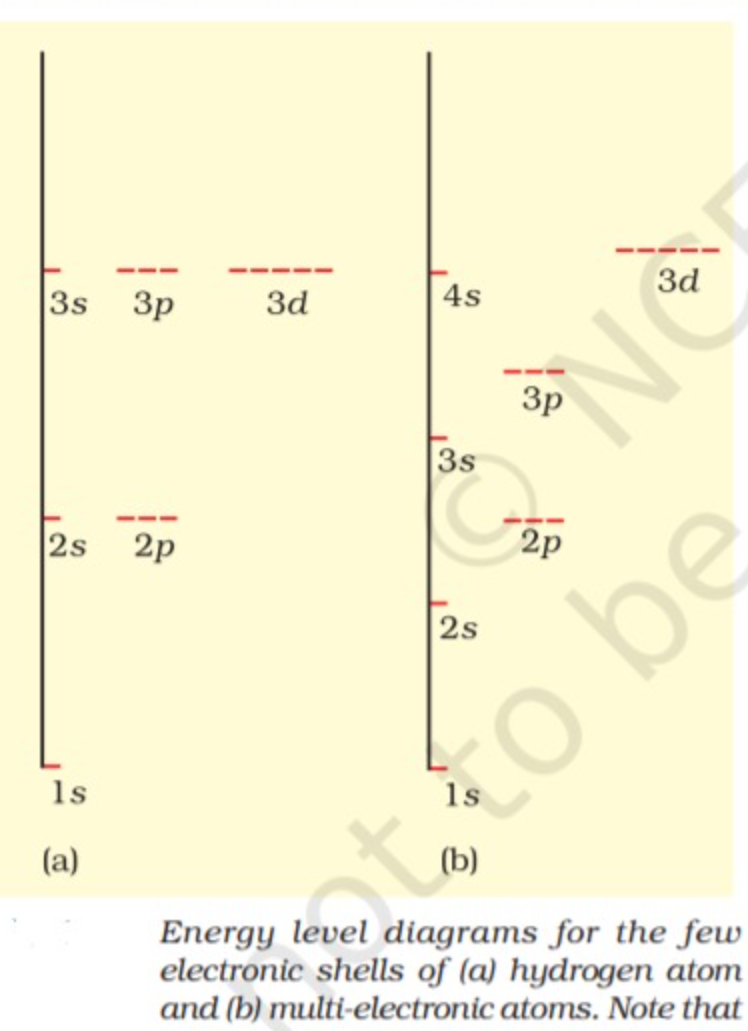

The reason for the above sequence is the:
(i) Mutual repulsion among the electrons in multielectron atoms .
(ii) The attraction between the negatively charged electron and the positively charged nucleus. Thus the stability of an electron in a multi-electron atom is because total attractive interactions are more than the repulsive interactions. On the other hand, the attractive interactions of an electron increases with an increase of positive charge (`Z_e`) on the nucleus
Concept of Effective Nuclear Charge (`Z_"eff"`)
1. Valence electrons in a multi electron system are attracted by nucleus and on the other hand repelled by the inner shell electron as well as the electron present in the same shell.
2. As a result of this attraction and repulsion effective attraction experienced by the test electron is less.
3. An electron present in the inner shell acts as a screen or shield electron for the outer electron from the nuclear force and is known as shielding electron.
4. According to Slater, effective nuclear charge depends on the fact that in which orbital electron is found, upon the shell and shape of the orbital in which the electron is present, s orbital shields the outer electrons from the nucleus more effectively as compared to electrons present in p orbital and p shields an electron better than d , even though all these orbitals are present in the same shell i.e. n is same. Order of Shielding Power is : s > p > d > f .
Note:1. The lower the value of (n + l) for an orbital, the lower is its energy. If two orbitals have the same value of (n + l), the orbital with lower value of n will have the lower energy.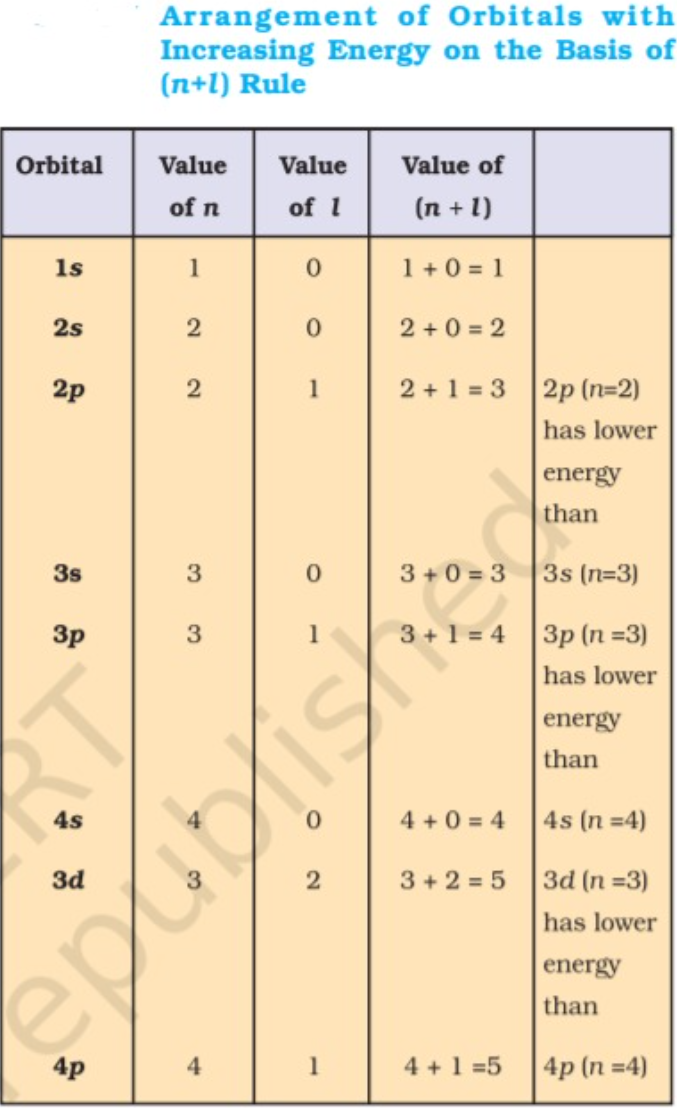

2. energies of the orbitals in the same subshell decrease with increase in the atomic number (`Z_(eff)`). For example, energy of 2s orbital of hydrogen atom is greater than that of 2s orbital of lithium and that of lithium is greater than that of sodium and so on, that is, `E_(2s) (H) > E_(2s) (Li) > E_(2s) (Na) > E_(2s)` (K).

Pauli's Exclusion Principle
According to this principle no two electrons can have the same set of four Quantum numbers. Now as we know that any electron is described by four Quantum numbers which are n,l,m and s so if two electrons are present in an orbital, they will have the same value of n, l and m but the value of s will be different. Thus we can conclude that an orbital can have a maximum of two electrons and these two electrons must have opposite spins so as to follow pauli's exclusion principle.
For Example If we have to write the values of n, l , m , s for `4s^2`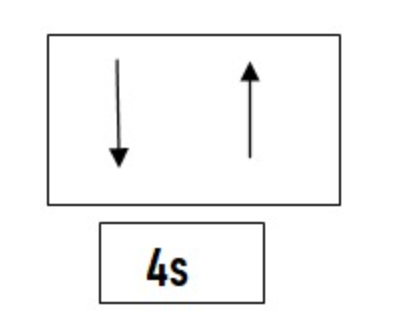
n = 4 `" "` l = 0 `" "` m = 0 `" "` s = `+1 / 2` , `- 1 / 2`
In this both the electrons are present in the same s subshell and hence 3 quantum numbers are the same but s is different.
(II) Aufbau Rule
Aufbau is German for ‘building up’ and above rule means that if an electron has to enter an orbital initially it will enter the orbital with the lowest energy and once the lowest energy orbital has been filled then it will go to the other higher energy orbital The energy of the orbitals is decided by the n + l rule.

In the ground state of atoms the orbitals are filled in order of increasing energy i.e the electrons will first occupy the lower energy orbital and then the next higher. The energy of the orbitals can be decided with the help of n+l rule as mentioned above.
For Example :1. Out of 4s and 5p which will be filled first?
Solution : In case of 4s`" "` n = 4, l = 0 using the n+ l rule we get 4 + 0 = 4
In case of 5p`" "` n = 5, l = 1 using the n+ l rule we get 5 + 1 = 6
As the value is lowest in case of 4s, it will be filled first.
Now what if the n + l value comes out to be the same.
For Example : 1. Out of 4s and 3p which will be filled first?
Solution : Now for 4s we know n + l = 4 , for 3p `" "` n = 3, l = 1 hence n + l = 4
now in such cases we see the value of 'n' smaller the value of n lower is the energy or vice versa, in this question 3p has a smaller value of n than 4s hence it will be of lowest energy and will be filled first.
(III)Hund's Rule of Maximum Multiplicity This rule states that the pairing of electron in the orbitals of same subshell does not occur till each orbital is singly occupied.
For Example :
Nitrogen Contains 7 electrons and its configuration can be written as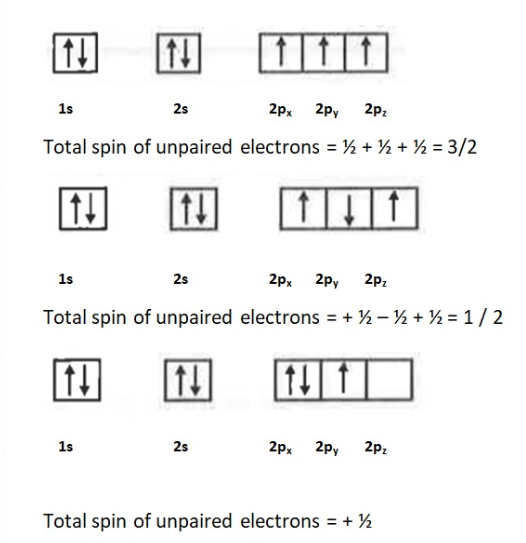

In the first case there are only three unpaired electrons with similar spin(Clockwise or anticlockwise) hence all have + `1/ 2 ` spin and it is the right way to represent them. In the second case the electrons do not have similar spins, and one spin cancels out the other and we get +1/2 as total spin and this configuration is incorrect.In the third case `2p_x` has two electrons whereas `2p_z` is empty, this is also in violation with Hund's Rule hence it is incorrect.
Only the first configuration is in accordance with the rule.

The distribution of electrons into different shells, sub shells and orbitals of an atom is called Electronic ConfigurationThe electronic configuration is represented by `nl^x`
n = Principal quantum number or no. of the shell
l = Azimuthal quantum number or no. of orbital/subshell (s,p,d,f)
x = no. of electrons
Let us see the electronic configuration of few elements.
Hydrogen - Z -1 `" "` E.C = `1s^1` `" "`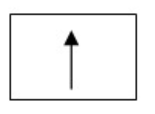
As the orbital has only electron it will be represented in this way
Helium - Z- 2 `" "`E.C = `1s^2` `" "`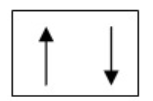
As the s-subshell has only two electrons they will be present in a single orbital.
Lithium - Z - 3 `" "` E.C = `1s^2 2s^1` `" "`
As the 1s subshell has two electron and 2s subshell has one electron it will be represented in the following manner
Berylium - Z - 4`" "` E.C = `1s^2 2s^2``" "`
As the 1s subshell has one electron and 2s subshell has two electron it will be represented in the following manner
Boron Z - 5`" "` E.C = `1s^2 2s^2 2p^1` `" "`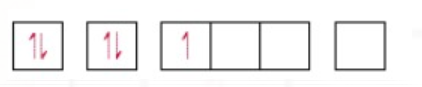
As the 1s subshell has one electron 2s subshell has two electron and 2p has one electron it will be represented in the following manner
Carbon Z - 6`" "` E.C = `1s^2 2s^2 2p^2`
Nitrogen Z - 7 `" "`E.C = `1s^2 2s^2 2p^3`
Oxygen Z - 8`" "` E.C = `1s^2 2s^2 2p^4`
Fluorine Z - 9 `" "` E.C = `1s^2 2s^2 2p^5`
Neon Z - 10 `" "` E.C = `1s^2 2s^2 2p^6`
Sodium Z - 11`" "` E.C = `[Ne] 3s^1`
(We can replace the initial configurations with the preceding Noble gases for the sake of simplicity like in this case we have used Neon)
Magnesium
Z- 12`" "` E.C = `[Ne] 3s^2`
Aluminium
Z - 13`" "` E.C = `[Ne] 3s^2 3p^1`
Silicon
Z - 14`" "` E.C = `[Ne] 3s^2 3p^2`
Phosphorous
Z - 15`" "` E.C = `[Ne] 3s^2 3p^3`
Sulphur
Z - 16`" "` E.C = `[Ne] 3s^2 3p^4`
Chlorine
Z - 17`" "` E.C = `[Ne] 3s^2 3p^5`
Argon
Z - 18`" "` E.C = `[Ne] 3s^2 3p^6`
Potassium
Z - 19`" "` E.C = `[Ar] 4s^1`
Calcium
Z - 20`" "` E.C = `[Ar] 4s^2`
Scandium
Z - 21`" "` E.C = `[Ar] 4s^2 3d^1`
Titanium
Z - 22`" "`E.C = `[Ar] 4s^2 3d^2`
Vanadium
Z - 23 `" "` E.C = `[Ar] 4s^2 3d^3`
Chromium
Z - 24`" "` E.C = `[Ar] 4s^1 3d^5`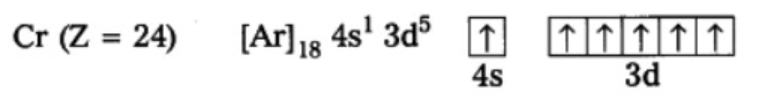
Chromium has exceptional configuration and the reason we will learn in the next segment.
Manganese
Z- 25 `" "` E.C = `[Ar] 4s^2 3d^5`
Iron
Z - 26 `" "` E.C = `[Ar] 4s^2 3d^6`
Cobalt
Z - 27 `" "` E.C = `[Ar] 4s^2 3d^7`
Nickel
Z- 28 `" "` E.C = `[Ar] 4s^2 3d^8`
Copper
Z - 29 `" "` E.C = `[Ar] 4s^2 3d^9`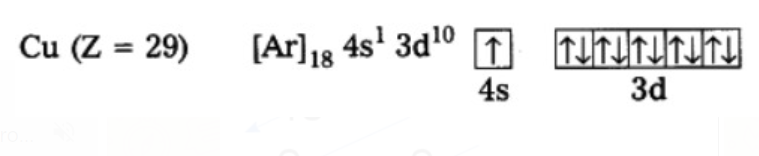
Copper also has exceptional configuration and the reason will be in the next segment.
Zinc
Z - 30 `" "` E.C = `[Ar] 4s^2 3d^10`

The ground state electronic configuration of the atom of an element always corresponds to the state of the lowest total electronic energy. The electronic configurations of most of the atoms follow the basic rules discussed in previous section. However, in certain elements such as Cu, or Cr, where the two subshells (4s and 3d) differ slightly in their energies, an electron shifts from a subshell of lower energy (4s) to a subshell of higher energy (3d), provided such a shift results in all orbitals of the subshell of higher energy getting either completely filled or half filled. The valence electronic configurations of Cr and Cu, therefore, are `3d^5` `4s^1` and `3d^10` `4s^1` respectively and not `3d^4` `4s^2` and `3d^9` `4s^2`. It has been found that there is extra stability associated with these electronic configurations.
Causes of Stability of Completely Filled and Half-filled Subshells
(i) Symmetrical Distribution of electrons : We know that symmetry leads to stability, thus the half filled and fully filled electronic configuration are more stable due to symmetrical distribution of electrons. For example The expected electronic configuration of Chromium is `" "` [Ar] `4s^2 3d^4` but the actual configuration is `" "` [Ar] `4s^1 3d^5` as one 4s electron jumps into the 3d orbital to give it a half filled configuration, and the configuration will be symmetrical.
(ii) Exchange Energy : When the electrons of parallel spin are present in degenerate orbitals(Same energy) they exchange their position, the energy released during this process is called Exchange Energy The no. of exchange is minimum when the orbitals are half filled or fully filled and more the exchange energy more is the stability.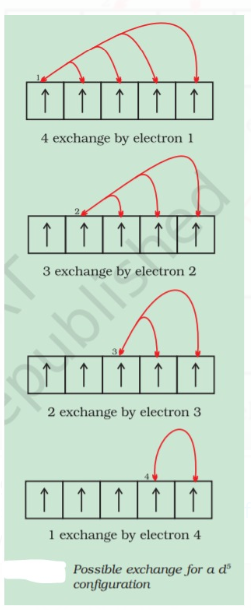

Atoms are the building blocks of elements. They are the smallest parts of an element that chemically react. earlier it was proposed that atom is the ultimate indivisible particle of matter. But later on , it was proved experimentally that atoms are divisible and consist of three fundamental particles: electrons, protons and neutrons.
Thomson in 1898 proposed that an atom consists of uniform sphere of positive electricity with electrons embedded into it. This model in which mass of the atom is considered to be evenly spread over the atom was proved wrong by Rutherford’s famous alpha-particle scattering experiment in 1909. Rutherford concluded that atom is made of a tiny positively charged nucleus, at its centre with electrons revolving around it in circular orbits. Rutherford model, which resembles the solar system, was no doubt an improvement over Thomson model but it could not account for the stability of the atom i.e., why the electron does not fall into the nucleus.
Bohr postulated that electron moves around the nucleus in circular orbits. Only certain orbits can exist and each orbit corresponds to a specific energy. Bohr calculated the energy of electron in various orbits and for each orbit predicted the distance between the electron and nucleus. Bohr model, though offering a satisfactory model for explaining the spectra of the hydrogen atom, could not explain the spectra of multi-electron atoms.
In Bohr model, an electron is regarded as a charged particle moving in a well defined circular orbit about the nucleus. The wave character of the electron is ignored in Bohr’s theory. An orbit is a clearly defined path and this path can completely be defined only if both the exact position and the exact velocity of the electron at the same time are known. This is not possible according to the Heisenberg uncertainty principle. Bohr model of the hydrogen atom, therefore, not only ignores the dual behaviour of electron but also contradicts Heisenberg uncertainty principle.
These quantized energy states and corresponding wave functions which are characterized by a set of three quantum numbers (principal quantum number n, azimuthal quantum number l and magnetic quantum number `m_l`) arise as a natural consequence in the solution of the Schrödinger equation. The restrictions on the values of these three quantum numbers also come naturally from this solution. The quantum mechanical model of the hydrogen atom successfully predicts all aspects of the hydrogen atom spectrum including some phenomena that could not be explained by the Bohr model. According to the quantum mechanical model of the atom, the electron distribution of an atom containing a number of electrons is divided into shells. The shells, in turn, are thought to consist of one or more subshells and subshells are assumed to be composed of one or more orbitals, which the electrons occupy. While for hydrogen and hydrogen like systems (such as `He^+`, `Li^(2+)` etc.) all the orbitals within a given shell have same energy, the energy of the orbitals in a multi-electron atom depends upon the values of n and l: The lower the value of (n + l ) for an orbital, the lower is its energy. If two orbitals have the same (n + l ) value, the orbital with lower value of n has the lower energy. In an atom many such orbitals are possible and electrons are filled in those orbitals in order of increasing energy in accordance with Pauli exclusion principle (no two electrons in an atom can have the same set of four quantum numbers) and Hund’s rule of maximum multiplicity (pairing of electrons in the orbitals belonging to the same subshell does not take place until each orbital belonging to that subshell has got one electron each, i.e., is singly occupied). This forms the basis of the electronic structure of atoms.